Download: Frac_dim.ela
File Includes:
Indicator - JRC Fractal Dim
Function - JRC_fractal_dim
Category: Fractals > JRC Fractals Dim
Description:
There is a weak and a strong way to measure the random quality of a time series.
The weak way is to use the random walk index (RWI). You can download it from the Omega web site. It makes the assumption that the market is moving randomly with an average distance D per move and proposes an amount the market should have changed over N bars of time. If the market has traveled less, then the action is considered random, otherwise it's considered trending.
The problem with this method is that taking the average distance is valid for a Normal (Gaussian) distribution of price activity. However, price action is rarely Normal, with large price jumps occuring much more frequently than a Normal distribution would expect. Consequently, big jumps throw the RWI way off, producing invalid results.
The strong way is to not make any assumption regarding the distribution of price changes and, instead, measure the fractal dimension of the time series. Fractal Dimension requires a lot of data to be accurate. If you are trading 30 minute bars, use a multi-chart where this indicator is running on 5 minute bars and you are trading on 30 minute bars.
Usage:
The following table shows how to interpret the results....
Fractal Dimen. Autocorrelation[1] Fractal Eff. Description
----------------------------------------------------------------------
2.0 -1.0 0.0 congestion
1.5 0.0 0.5 random walk
1.0 1.0 1.0 trend
----------------------------------------------------------------------
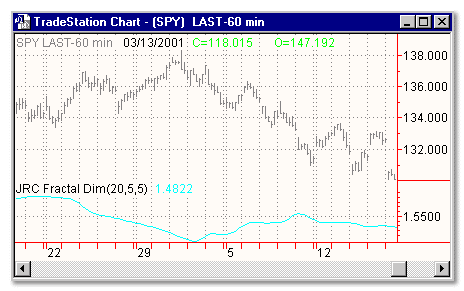
Inputs:
SIZE - size of fractals, typically 10 bars wide
COUNT - number of fractals to use, typically 2
SMOOTH - simple average smoothing length
Try using the default values first.
Remember two important points:
1) Trend is STRONGER when the indicator is LOWER. If this is confusing, you can convert Fradtal Dimension to a trend efficiency index (like Kaufmann's efficiency ratio) this way:
Trend Efficiency = 2 - Fractal Dimension
2) Maxbarsback must be set greater than SIZE*COUNT
EasyLanguage Code:
INPUTS: SIZE(20), COUNT(5), SMOOTH(5) ;
VALUE1 = JRC_FRACTAL_DIM ( SIZE , COUNT ) ;
PLOT1 ( AVERAGE(VALUE1,SMOOTH) , "" ) ;